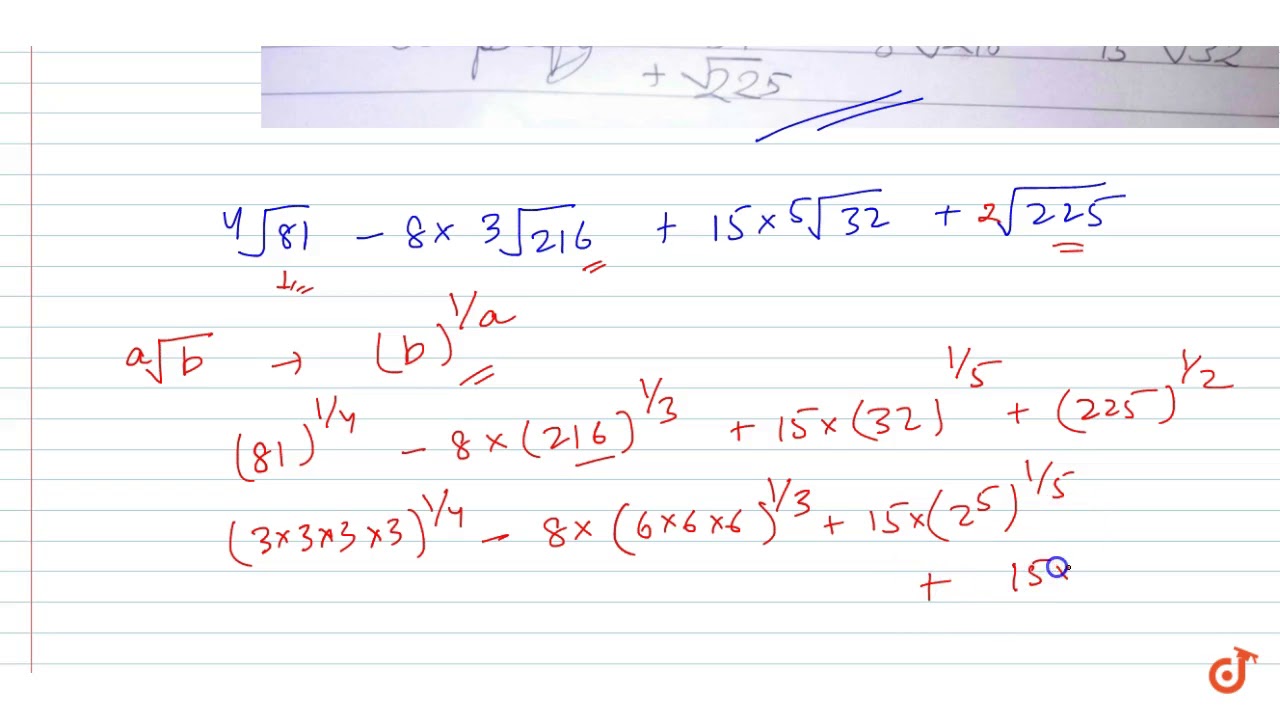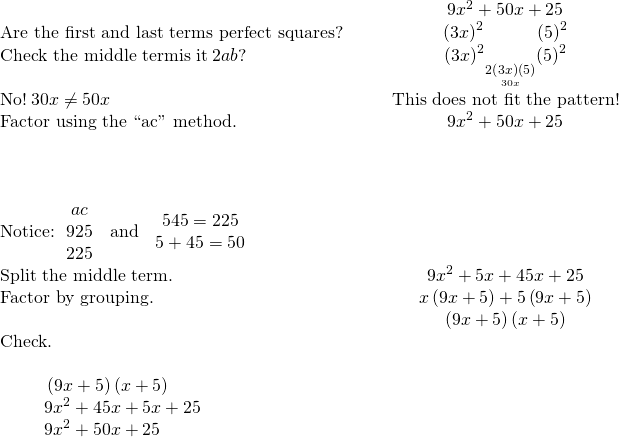Square Root Of 225 By Repeated Subtraction Method

Finding the square root of a number by repeatedly subtracting successive odd numbers from the given square number till you get zero is known as repeated subtraction method.

Square root of 225 by repeated subtraction method.

Since a square root of a number must equal that number when multiplied by itself. 49 1 48. A square root is only possible for even number of zeros. 24 11 13.

First check whether the given number is a perfect square number or not. 48 3 45. So for finding square root we start subtraction from 1 and continue until it reaches zero. Find square root of 225 by repeated subtraction method.

To find square root we subtract consecutive odd numbers from number till we obtain 0 square root total numbers subtracted let s take an examplesuppose we need to find 81square root of 8181 1 8080 3 7777 5 7272 7 6565 9 5656 11 4545 13 3232 15 1717 17 0since aft. 17 17 0. 32 15 17. 13 13 0.

225 1 224 step 2. The steps to find the square root of 49 is. 221 5 216. 72 7 65.

77 5 72. 81 1 80. When 25 is multiplied by 25 we get 25 as a result. 1 cannot have a square root at least not a real one because any two numbers with the same sign positive or negative when multiplied will equal a positive number.

80 3 77. Example 1 find the square root of 144 by the subtraction method. Find the square root of 49 using the repeated subtraction method. Two same square roots are multiplied to give a non square root number.

Basic methods of finding a square root repeated subtraction method. 65 9 56 56 11 45. 2 2 4 and 2 2 4. The result 0 is obtained in the 7th step.

Two square roots can be multiplied. 40 7 33. 45 13 32. Hence the square root of 49 49 is 7.

Let us consider another example to find the square root of 81 by repeated subtraction. 45 5 40. 224 3 221 step 3. Let us find the square root of 81 by repeated subtraction method.

33 9 24. Every natural number squared can be written as the sum of consecutive odd natural numbers starting from zero.